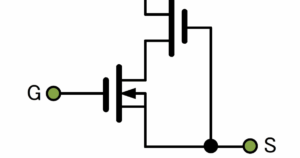
2ポール位相補正2

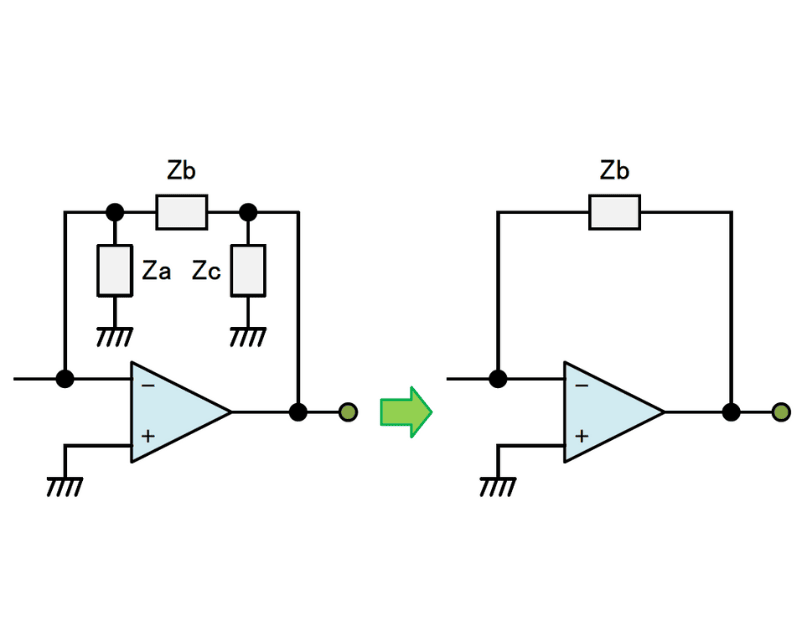
2ポール位相補正は色々な形式があるのですがその一つに図1があります。その等価回路は図2になります。

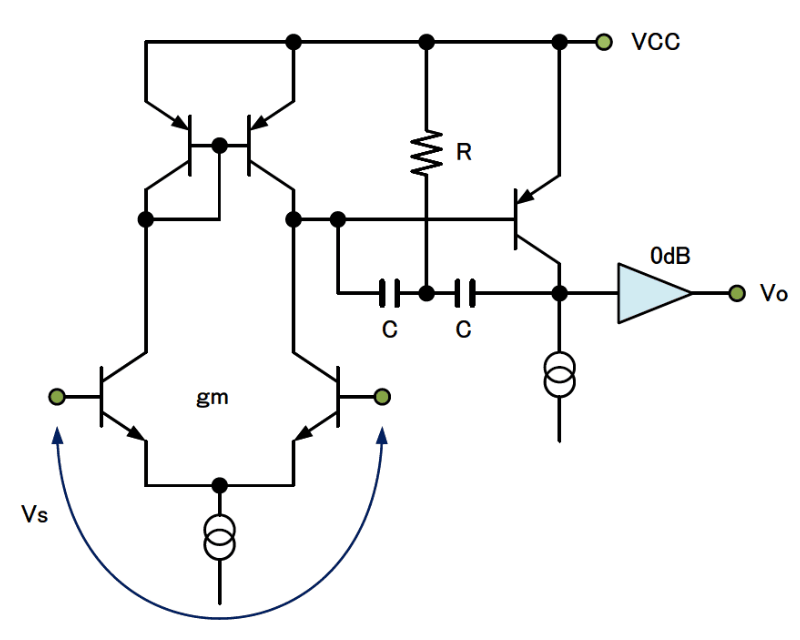
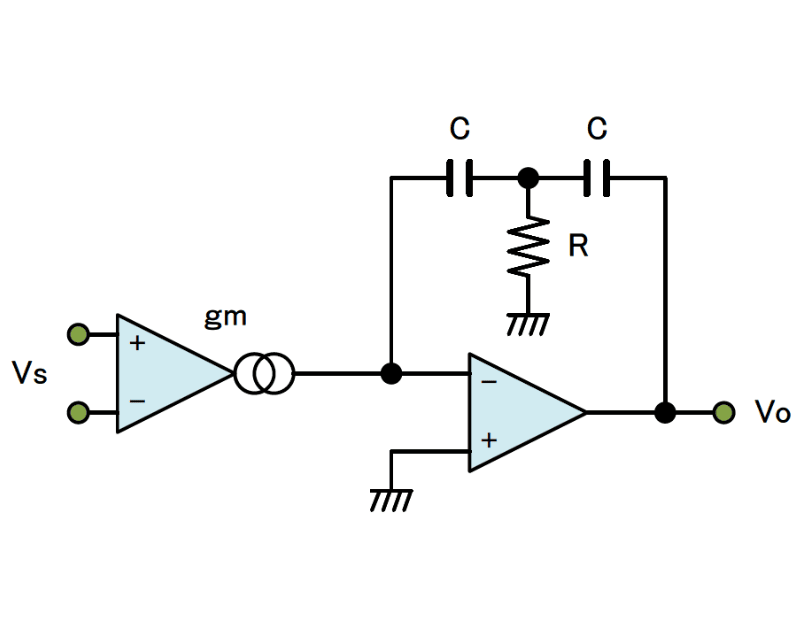
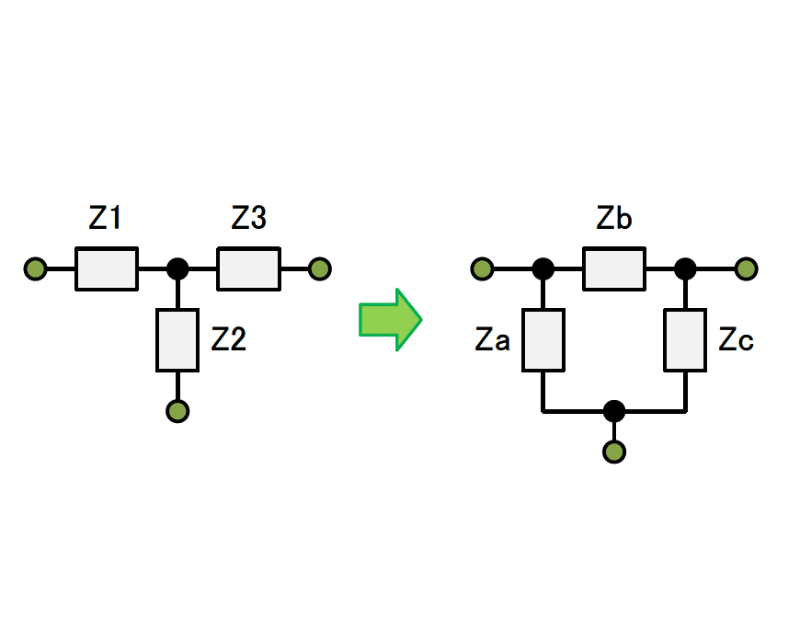
図2の2段目の帰還回路は、そのままキルヒホッフで解くことが出来ますが結構面倒です。そこで図3の様にY→Δ変換します。そしてZaとZcは省略可能なので最終的に図4のZbだけが残ります。さてそのZbですがY→Δの変換公式（省略）から式1となります。

$$
Z_b=\frac{2}{sC}+\frac{1}{R(sC)^2}
=\frac{1}{s^2RC^2}\left(1+s\,2CR\right)
\quad（式1）
$$

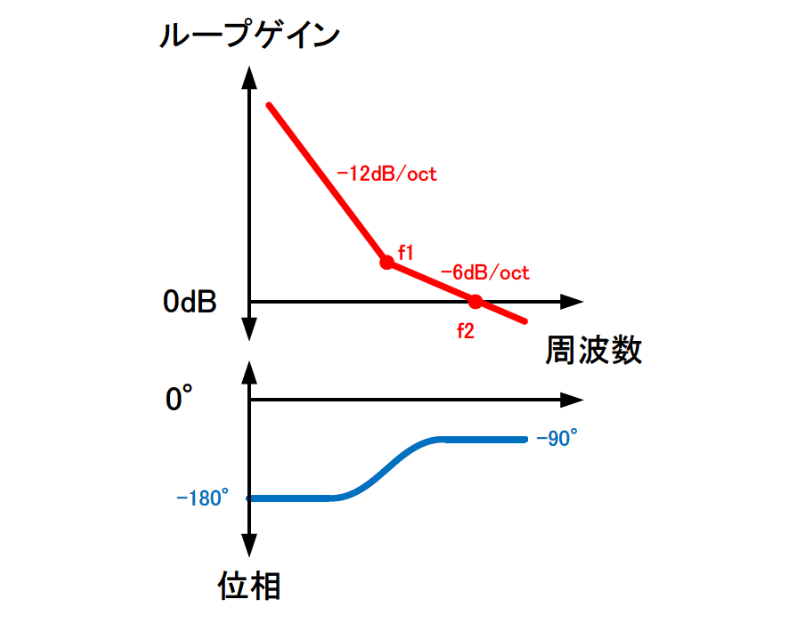
アンプとしての出力Ｖoは、式2の初段のgmと2段目のZbとの積になります。また図5の-12dB/octから-6dB/octへの転換点f1は式3です。（s=jω）

$$
V_o=g_m\cdot\frac{1}{s^2RC^2}\left(1+s\,2CR\right)\cdot V_s
\quad（式2）
$$

$$
f_1=\frac{1}{2\pi\,2CR}
\quad（式3）
$$

周波数がf1点より高くなると、式2は式4に簡略化することが出来ます。式中のＣ/２は図2のＣが2個直列になる事からも理解できます。図5のf2点はループゲインが0dBになる周波数なので、それを踏まえて式4から式5を得ます。

$$
V_o=g_m\cdot\frac{1}{2\pi f\left({\Large \frac{C}{2}}\right)}\cdot V_s
\quad（式4）
$$

$$
f_2=g_m\cdot\frac{1}{2\pi\left({\Large \frac{C}{2}}\right)}
\quad（式5）
$$

2ポール位相補正によるアンプ設計は、f1とf2を決めるだけで簡単に設計することが出来ます。ポイントはf1とf2は最低でも5倍以上離すことです。
私は2ポール位相補正の考え方を発展させ、OPアンプ3個を直列にして一つのアンプとして機能する使い方もよく行っております。